if we sort, we can iterate from j = i-1 to 0 and break once its divisible. has a 10x faster runtime for most.
dp = [1] * len(nums)
nums.sort()
res = 0
for i in range(1, len(nums)):
for j in range(i-1, -1, -1):
if nums[i] % nums[j] == 0:
dp[i] = dp[j] + 1
res = max(res, dp[i])
break
0.04176688194274902 (given solution)
0.003387928009033203 (above solution)
27
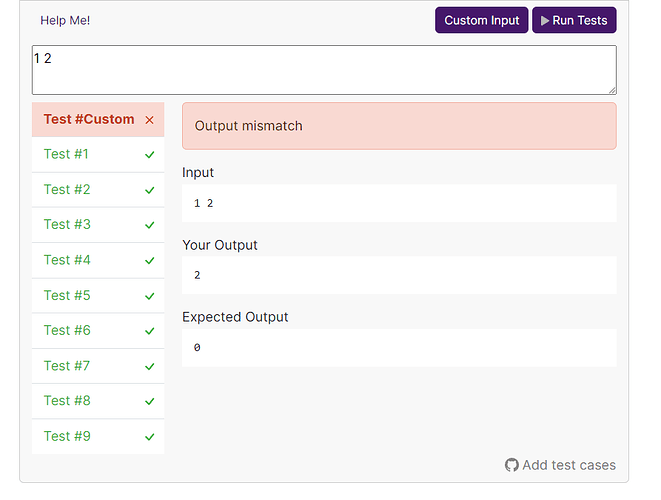
it is faster but it is incorrect ![]()
take a set “1 2 3 4 8 16 32 33 1056 (= 32*33)”
a set ending up with 32 has 6 elements and a set ending with 33 has only 3 elements.
Your algorithm would determine that the largest set including number 1056 has size 4 instead of 7.
Here is a method that utilizes breaking early correctly in C#:
nums.Sort();
var maxSubsets = new List<int>();
int largestSubset = 1;
for (int i = 0; i < nums.Count; i++) {
int maxSubset = 0;
for (int j = i - 1; j >= 0; j--) {
if (nums[i] % nums[j] == 0 && maxSubsets[j] > maxSubset) {
maxSubset = maxSubsets[j];
if (maxSubset == largestSubset) {
largestSubset++;
break;
}
}
}
maxSubsets.Add(maxSubset + 1);
}
return largestSubset;
Please rewrite the solution explanation since it is poorly worded. Also please add the Top-Down Solution as well. Here is mine. Using the same mathematical logic as the bottom up solution, sort the list and use the Longest Increasing Subsequence template to solve the Problem. Here is my python solution for it:
from typing import List
def find_largest_subset(nums: List[int]) → int:
def dfs(i, nums, maxCount, visited):
if i == 0:
return 0
if i in visited:
return visited[i]
longest = dfs(0, nums, maxCount, visited) + 1
ni = nums[i - 1]
for j in range(1, i):
nj = nums[j - 1]
currLongest = dfs(j, nums, maxCount, visited)
if ni % nj == 0:
longest = max(longest, currLongest + 1)
maxCount[0] = max(maxCount[0], longest)
visited[i] = longest
return longest
visited = {}
maxCount = [0]
nums.sort()
dfs(len(nums), nums, maxCount, visited)
return maxCount[0]
if name == ‘main’:
nums = [int(x) for x in input().split()]
res = find_largest_subset(nums)
print(res)
Are you sure your code works? It appears that your code returns the longest subset with nums[i - 1] included for the set size i. However, for size i, it might be the case that i - 1 might not be included. For example, 1 2 4 8 9.
Simple Java solution:
public static int findLargestSubset(List<Integer> nums) {
Collections.sort(nums);
int[] dp = new int[nums.size()];
for(int i = dp.length-1; i >=0; i--) {
dp[i] = 1;
for(int j = i+1; j<dp.length; j++) {
if (nums.get(j)%nums.get(i) == 0) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
return dp[0];
}
Hi HonyYi,
I was interested in your method as it does not involve having to find a max along the length of dp. However, I have been able to find a counter example that causes your method to fail and hence I do think find the max along dp is still necessary. Please try the numbers {2,3,9,15}
Python code in this article is such a shameful mess, for instance what happens to max_len in the frist snippet is entirely incorrect
Indices can also be optimised to avoid having offsets, which is way easier to understand
def find_largest_subset(nums: List[int]) -> int:
nums.sort()
n = len(nums)
dp = [1] * n
max_len = 1
for i in range(n):
for j in range(i):
if nums[i] % nums[j] == 0:
dp[i] = max(dp[i], dp[j] + 1)
max_len = max(max_len, dp[i])
return max_len